今日は式の変形について解説していきたいと思います🎤
この記事を読むとこんな事が分かります📖
式の変形の必要性
式の変形の仕方
式の変形の実用例
先に記事にした切削速度や切削送り速度などを使用する際必ずしも式の通りに使う場面ばかりではないですよね❔
「=のこっち側にあるこの値が求めたいんだけど…。」
そんな時に式の変形を覚えておくと、とても便利です❕
三角関数などを使って計算する場合なんかにも使います△
式の変形はみなさん中学生の時に一度は習っているので今回の記事を見て思い出していただけたらと思います☆
数学の授業ではないので実際に仕事などで使える様に簡単に分かりやすく説明していきますので最後まで読んでいってもらえたら嬉しいです❕
式の変形の必要性
切削速度を求める式
V=π×D×N/1000
切削送り速度を求める式
F=N×fz×z
などの基本的な式は目にした事があると思います。
しかし実際には切削速度を求めたい時や回転数を求めたい時、切削送り速度を求めたかったり、1刃当たりの送り量を求めたかったりと様々な場面が出てくると思います。
機械加工を行っていく中で他にも計算して求めなければならない値はたくさん出てきます💧
しかし求める可能性がある値の式を全て覚えておくのは大変です💦
例えば
切削速度を求める式
V=π×D×N/1000
回転数を求める式
N=V×1000/π×D
工具径を求める式
D=V×1000/π×N
この3つの式はどれも同じ式を変形しているものです。
全部を覚えて求めたい値に合わせて使い分ける方法でもいいと思いますが、私は覚えてられない自信があります(笑)
その場で覚えたとしても時間が経つにつれて1部忘れてしまったり、勘違いしてしまったりする可能性があります😔
そこで「式の変形」を使います!
「ベースの式」と「式の変形の仕方」の2つを覚えておけば他の式を覚える必要はありません😀
「式の変形の仕方」は違う公式にも使い回しが可能なのでどれも「ベースの式」のみ覚えればいいことになります!
私も含めて覚えるのが苦手な方にとっては、とても便利だと思います👍
式の変形の仕方
式の変形をやっていく前にルールの確認をしていきます。
①「=」を挟んで左右に同じことをすれば式は成り立つ
例として
10=10
この式の左右に同じ数値を+−×÷しても成り立ちます!
2+10=10+2
12=12
2×10=10×2
20=20
こんな感じです!
式のルールは以上✋
「あれ?中学校で習った時こんなだったっけ?」
っとお思いの方がいるかもしれませんが学校などでは計算の効率を上げる為に色んな手法を教えています!
でも実はそんなに複雑ではないので混乱を避ける為にここでは基本ルールしか使いません。
それでは実際に式の変形をやっていきたいと思います。

馴染みのあるこの式を使っていきます
切削速度(V)を求める式を回転数(N)を求める式に変形していきます
それではルール通りに左右に同じことをしていきます
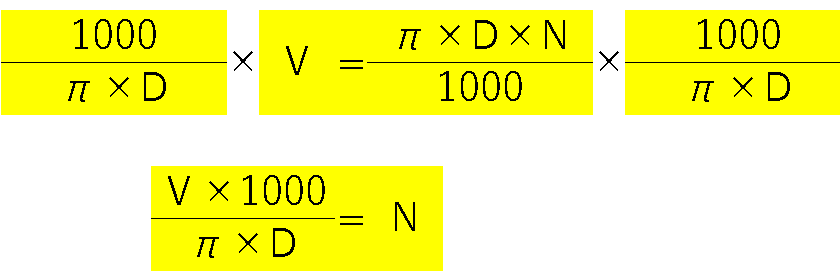
こんな感じです😃
「コレジャワカラナイヨ…。」
って人の為に詳しく説明していきます👍
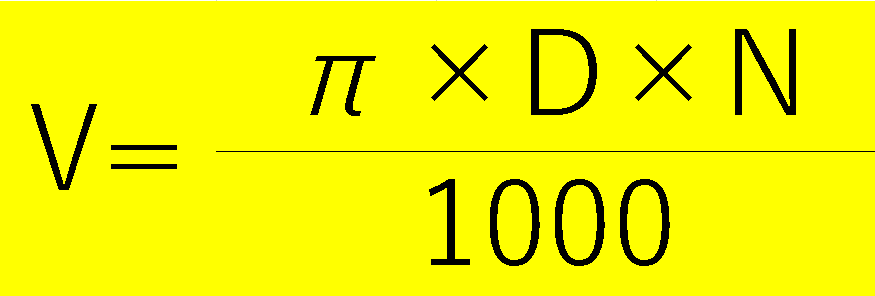
まずこの式の表現をかえてみます
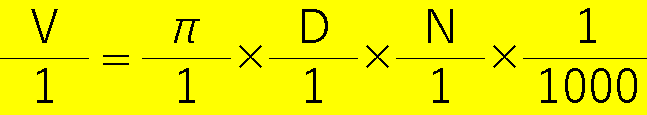
一つ一つに分解して、分数で表現しました❕
次に左右に同じ事をしていきます
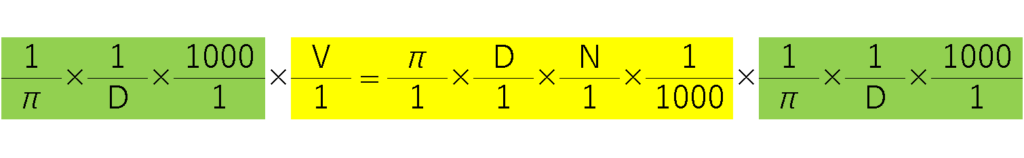
これを計算した状態にします

さらに分母と分子が同じものは「1」になるので(例 5/5=1)

こうなります
そして最後に右側を計算して(Nを1で割って、1を3回掛ける)
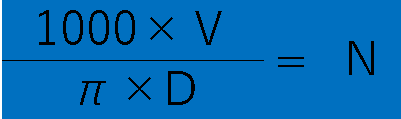
これで回転数を求める式になります

学校などでは単純に「残したい部分以外の分母と分子を反対にして逆側に持っていく」
なんて教え方もしていますね
式の変形の実用例
それでは実際に数値を求めてみましょう

切削速度と工具径から回転数を求める場合

このようになります
①分かっている数値を代入
②計算できる所を先に計算
③右側を求めたいNだけにするために左右に同じ数値を掛ける

④数値だけになった左側を計算
⑤回転数(N)が求められる
次は1刃当たりの送り量を求める場合


こんな風に計算します
終わりに
式の変形は他にも必要な場面が出てくると思います
そんな時は1つだけのルールを忘れずに確実に手順を踏んでやっていけばできるはずです
もし分からなくなってしまったら、またこの記事を見直してみてください
この記事が少しでも皆さんの役に立てたら嬉しいです
それではまた😃👋

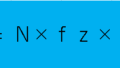
コメント